4.2. Экологическое моделирование и прогнозирование

Условно можно считать, что математическая экология (математическое моделирование и прогноз экологических процессов) возникла не с появлением экологии как науки, а значительно раньше. Например, известное моделирование плодовитости кроликов (1228 г., итальянский математик Фибоначчи) представляет одну из первых попыток математического прогноза динамики биологических процессов.

Первые математические модели учитывали закономерности естественного развития экологических систем. Полагалось, что компоненты экосистем, взаимодействуя, стремятся к стабильности своего системного образования и подчиняются законам эволюции. Под стабильностью экосистемы понимается ее способность к изменению своей структуру без разрушения системы в целом, а под сохранением - способность сохранять се основные характеристики. Экосистема в целом является саморегулпруемым комплексом, который стремится достиг путь стабильного состояния. Это возможно благодаря наличию как прямых, так и внутренних или внешних обратных связен. Простое саморегулирование, основанное па отрицательных обратных связях, осложняется наличием вторичных реакции и существованием предельных воздействий на экологические объекты.

В дальнейшем появились модели техносферы и модели, учитывающие антропогенное воздействие на компоненты планетарной экосистемы с проведением численных экспериментов и формированием качественных и количественных прогнозов. Модели стали базироваться на массовых данных динамического контроля, которые в той или иной степени отвечали требованиям пространственно-временной, качественной и количественной репрезентативности. При наличии обратных связен равновесие экосистемы имеет многозначный характер:

- стабильное равновесие, когда имеет место тенденция системы реставрировать условия предыдущего равновесия, которые были нарушены извне;

- нестабильное (дискретностабильное) равновесие, когда незначительное внешнее воздействие ведет к изменениям, заканчивающимся достижением нового устойчивого равновесия;

- динамическое равновесие - режим сбалансированных колебаний системы относительно постоянно развивающихся во времени и в определенном направлении условии функционирования системы, причем амплитуда этих колебании значительно превышает размах изменений среднего состоянья системы.

Время, необходимое для перехода системы из неравновесного состояния, вызванного антропогенными или естественными причинами, в повое или прежнее равновесное состояние, называют временем релаксации. Время релаксации зависит от устойчивости и состояния элементов системы, структуры системы, направленности экологических Изменений.

Системный экологический анализ позволяет исследовать характер, формы и масштабы экологических взаимосвязей и взаимодействий, проанализировать устойчивость и адаптацию объектов экосферы. В качестве инструментария системного экологического анализа наиболее часто используют математическое и физическое моделирование, методы оптимизации, теорию множеств и преобразовании и др.

В настоящее время существует множество методов прогнозирования. Их различают по количественной или качественной природе, точности, надежности, применяемому математическому аппарату, характеристикам объекта прогнозирования и др. В процессе развития прогностика шла эмпирико-индуктивным путем, т. е. закономерности формулировались на основе анализа и обобщения методов прогнозирования определенных объектов.

Методы экологического моделирования можно условно разделить на физические и математические. При физическом моделировании изучаемое явление воспроизводится в том или ином масштабе с сохранением его физической природы. Математическое моделирование представляет собой способ исследования экологических явлений путем изучения процессов, имеющих различное физическое содержание, но описываемых одинаковыми математическими соотношениями. Важным моментом является составление математической модели на основании формализованной (содержательной) схемы изучаемого явления. При этом выделяются сведения, непосредственно характеризующие объект наблюдения, производится постановка цели и задач исследования с перечнем искомых величин и требований к ним, задаются начальные условия. Решение математических моделей может осуществляться аналитически, численными методами, на аналоговых и цифровых вычислительных машинах. Математическая модель сложной системы (куда относят экологические системы) состоит из математических моделей подсистем, их элементов и математических моделей взаимодействуя между подсистемами. Процесс построения моделей экологических объектов является трудоемким и требует от разработчиков как знаний об объекте моделирования, так и навыков в системотехнике и моделировании.

Основным признаком отнесения системы к сложной является содержание в ней процесса решения (а следовательно, наличие цели). Необходимо также наличие следующих признаков:

- множество взаимосвязанных и взаимодействующие элементов;

- многофакторность цели;

- возможность разбиения системы на подсистемы;

- управление множеством информационных, энергетических, вещественных потоков в системе;

- взаимодействие с внешней средой.

Условное изображение объекта сложной экологической системы представлено на рис. 4.12.

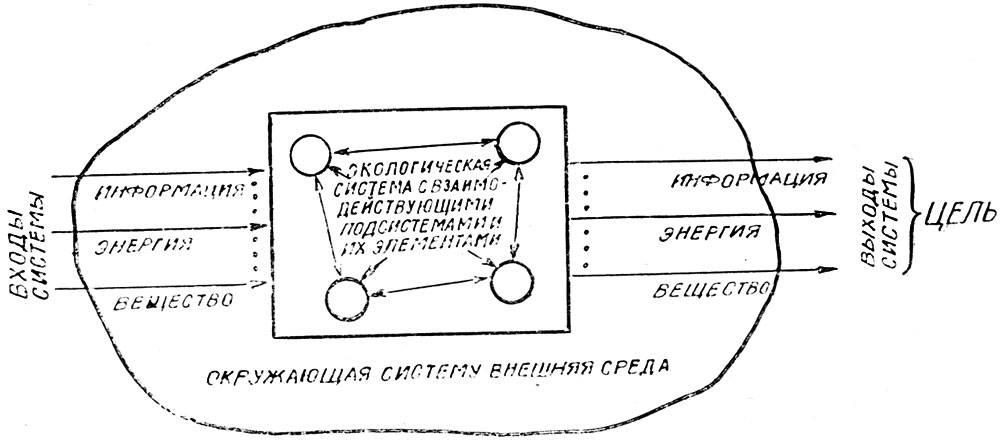
Рис. 4.12. Структурно-функциональная схема объекта сложной экологической системы

При современном экологическом состоянии актуальное значение приобретает количественная оценка состояния объектов контроля и управления. Естественным желанием исследователей является возможность получать оценку по одному обобщенному (интегральному) показателю, хотя набор подобных показателей видится наиболее полной характеристикой. Полный набор интегральных показателей наиболее качественно будет характеризовать экологическое состояние на альтернативном (да - нет) или множественном (относительные или абсолютные значения состояния объекта) уровнях.

Известен ряд зависимостей потоков вещества и энергии в экосистемах, но мало известно об информационном взаимодействии. Выявление информационных законов в системе живого и неживого позволит выявить дополнительные управляющие воздействия и управляемые последствия, для чего необходимо создание обновляющихся баз данных.

Математическое моделирование экосистем является научным направлением, которое становится действенным аппаратом познания экологических процессов, приближает к осуществлению практики управления ими. Причем математическое моделирование и экспериментальные наблюдения взаимно дополняют и развивают друг друга.

Первый тип моделей основан на фундаментальных законах материального мира (законы сохранения энергии, массы, количества движения, переноса, трансформации и др.). Исследователь проводит отбор наиболее существенных законов для конкретного объекта, осуществляет их формализованную запись, решает записанные уравнения и производит интерпретацию получаемых решений. К этому перечню зачастую добавляется процесс верификации моделей.

Подобные модели содержат в себе информацию как априорную, заключенную в структуре математической модели (тип дифференциального, интегрального, разностного, балансового или другого уравнения), так и информацию, содержащуюся в параметрах (коэффициентах) модели, которые определяются из опытных данных. Необходимо отметить, что и при отсутствии натурных данных о коэффициентах исследование решений математических уравнений модели позволит получить качественные, прогностические результаты.

В качестве примера математической модели пространственной турбулентной диффузии примесей в атмосфере или водной среде можно использовать дифференциальное уравнение в следующем виде:

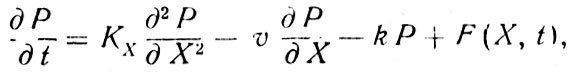
где t - время;

X - координата;

Р - концентрация примеси в объеме среды;

К_Х - коэффициент одномерной продольной диффузии (обмена);

υ - средняя скорость потока в среде;

k - коэффициент неконсервативности примеси (коэффициент, определяющий изменение концентрации примеси в среде за счет физико-химических превращений примеси; коэффициент самоочищения среды);

F(X, t) - пространственно-временная функция, описывающая источник примеси.

Отметим, что данное уравнение может усложняться за счет многомерности, многофакторности, разнообразия граничных и начальных условий, специфики среды, примесей и других факторов, а упрощение достигается, например, при возможности неучета функции источника примеси (F=0) или стационарности процесса поступления примеси в среду, т. е. δυ/δt=0, F(X, t)=F (X) при постоянстве скорости пли коэффициента обмена К_Х. Отметим, что рост коэффициента К_Х означает замедление обмена, т. е. вредные примеси будут стремиться к накоплению, и при* превышении норм самоочищения будет наблюдаться процесс дегенерации среды.

В качестве примера математической модели закономерностей формирования кислорода в придонном слое внутреннего водоема можно использовать дифференциальное уравнение в таком виде (предполагается, что поступление кислорода из вышележащих слоев в придонный слой происходит с постоянной скоростью):

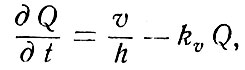
где Q - концентрация растворенного кислорода в придонном слое;

δQ/δt - скорость изменения содержания кислорода в придонном слое;

υ - скорость поступления кислорода в придонный слой;

h - толщина придонного слоя;

k_υ - коэффициент биохимического потребления кислорода водой и осадками.

Решение этого уравнения относительно величины υ представимо в виде следующего выражения:

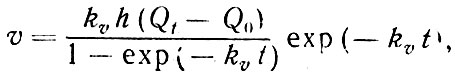
где Q₀ и Q_t - концентрация растворенного кислорода придонного слоя в начальный и конечный момент вертикального водообмена.

Зная или задаваясь значениями k_υ и h, контролируя датчиками содержание кислорода Q₀ и Q_t можно определять величину υ. При прогнозировании динамики величины υ можно варьировать значения как k_υ и h, так и Q₀ и Q_t

Решая задачу прогнозирования минерализации внутренних водоемов на основании уравнений солевого и водного баланса, можно получить упрощенную расчетную формулу ожидаемой средней минерализации воды

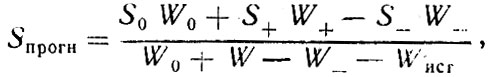
где S₀, S₊, S_- - средние значения минерализации водоема в начале расчетного периода, притоковых и стоковых вод;

W₀, W₊, W_- - объем водоема в начале расчетного периода, объем притоковых и стоковых вод;

W_исп - потери воды на испарение с поверхности водоема за расчетный период.

Трудности первого типа моделирования заключаются, с одной стороны, в неадекватности упрощенной модели ее реальному образу, а с другой стороны, в сложности обозримого представления реального образа многопараметрической моделью. К этим затруднениям присовокупляется влияние в реальной экологической ситуации случайных трудноучитываемых факторов, что делает головоломным формирование правдоподобных гипотез.

В результате преодоления этих сложностей получил развитие второй тип математических моделей, основанных на установлении закономерностей функционирования экологических систем путем статистического выявления взаимосвязей в этих системах или объектах. Разработка подобных моделей заключается в выборе метода статистического анализа, планировании процесса получения данных контроля, компоновке данных об экологической системе, алгоритмировании и расчете компьютерными средствами статистических соотношений. Изменение закономерностей развития экологической ситуации требует повторения описанной процедуры, но уже в новом качестве.

Статистическое нахождение математической модели включает в себя выбор вида модели и определение ее параметров. Причем искомая функция может быть как функцией одной независимой переменной (однофакторной), так и многих переменных (многофакторной). Задача выбора вида модели - задача неформальная, т. к. одна и та же зависимость может быть описана с одинаковой погрешностью самыми различными аналитическими выражениями (регрессионными уравнениями). Рациональный выбор вида модели может быть обоснован при учете ряда критериев: компактность (например, описанная одночленом или многочленом), интерпретируемость (возможность придания содержательного смысла коэффициентом модели) и др. Задача расчета параметров выбранной модели зачастую чисто формальная и осуществляется на ЭВМ.

Формируя статистическую гипотезу об определенной экологической системе, необходимо иметь массив разнообразных данных (базу данных), который может быть неоправданно велик. Адекватное представление о системе связано в этом случае с отделением несущественной информации. Сокращению могут подлежать как перечень (тип) данных, так и количество данных. Одним из методов осуществления подобного сжатия экологической информации (без априорных предположений о структуре и динамике наблюдаемой экосистемы) может стать факторный анализ. Сокращение данных проводят методом наименьших квадратов, главных компонент и другими с использованием в дальнейшем, например, кластерного анализа.

Отметим, что первичная экологическая информация обладает в той или иной степени следующими особенностями:

- многомерностью данных;

- нелинейностью и неоднозначностью взаимосвязей в исследуемой системе;

- погрешностью измерений;

- влиянием неучтенных факторов;

- пространственно-временной динамикой.

При решении первой задачи (выбор вида модели) полагают, что известны m входных (х₁, х₂, ..., х_m и n выходных (y₁, y₂, ..., y) данных. В этом случае возможны, в частности, следующие две модели в матричной записи:

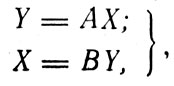
где X и Y - известные входные (выходные) и выходные (входные) параметры экологического объекта ("черного ящика") в векторной форме записи; А и В - искомые матрицы постоянных коэффициентов модели (параметров модели).

Наряду с указанными моделями рассматривается более общий вид статистического моделирования:

CY=F=DX,

где F - вектор скрытых влияющих факторов; С и D - искомые матрицы коэффициентов.

При решении экологических задач целесообразно использовать и линейные и нелинейные по переменным математические модели, т. к. многие экологические закономерности мало исследованы. В результате будут учтены многомерность и нелинейность моделируемых взаимосвязей.

На основе обобщенной модели можно выделить внутренние скрытые факторы изучаемых экологических процессов, которые не известны инженеру-экологу, но их проявление отражается на компонентах векторов X и Y. Эта процедура наиболее целесообразна в случае, когда между величинами X и Y ре наблюдается строгой причинно-следственной связи. Обобщенная модель с учетом воздействия скрытых факторов устраняет определенное противоречие между двумя моделями с матрицами А и В, когда фактически две различные модели могли бы быть использованы для описания одного и того же экологического процесса. Это противоречие вызвано противоположным смыслом причинно-следственной зависимости между величинами А и Y (в одном случае X - вход, а Y - выход, а в другом - наоборот). Обобщенная модель с учетом величины F - списывает более сложную систему, из которой обе величины X и Y являются выходными, а па вход действуют скрытые факторы F.

Немаловажным при статистическом моделировании является использование априорных данных, когда еще в процессе решения могут быть установлены некоторые закономерности моделей и сужено их потенциальное количество.

Предположим, необходимо составить модель, с помощью которой за 24 ч можно численно определить плодородие определенного типа почвы с учетом ее температуры Т и влажности W. Ни пшеница, ни яблоня за 24 ч дать урожай не могут. Но для пробного сева можно использовать бактерии с коротким жизненным циклом, а в качестве количественного критерия интенсивности их жизнедеятельности пользоваться количеством Р выделенного СО₂ в единицу времени. Тогда математическая модель исследуемого процесса представляет собой выражение

P=P₀f(T, W),

где P₀ - численный показатель качества почвы.

Кажется, что у нас нет никаких данных о виде функции f(T, W) потому, что у инженера-системотехника нет нужных а грономических знаний. Но это не совсем так. Кто не знает, что при Т≈0°С вода замерзает и, следовательно, СO₂ выделяться не может, а при 80°С происходит пастеризация, т. е. большинство бактерий погибает. Априорных данных уже достаточно для утверждения, что искомая функция имеет квазипараболический характер, близка к нулю при Т=0 и 80°С и имеет экстремум внутри этого интервала температур. Аналогичные рассуждения относительно влажности приводят к фактофиксации максимума экстремума искомой функции при W=20% и приближении ее к нулю при W=0 и 40%. Таким образом, априори определен вид приближенной математической модели, а задачей эксперимента является лишь уточнение характера функции f(T, W) при Т=20 ... 30 и 50 ... 60°С, а также при W=10 ... 15 и 25 ... 30% и более точное установление координат экстремума (что уменьшает объем экспериментальных работ, т. е. объем статистических данных).

Определение параметров регрессионных моделей производят преимущественно методом наименьших квадратов, методом главных компонент и их разновидностями.

Потребность в долгосрочном прогнозировании поведения сложных экологических систем вызвала создание третьего типа математического моделирования - имитационного, вобравшего в себя идеи первого типа и опыт построения второго типа моделей. Суть имитационного моделирования заключается в изучении сложной математической модели с помощью экспериментирования с моделью и обработке результатов этих экспериментов. Имитация позволяет воссоздавать причинно-следственные связи экологических явлений и процессов, предоставляя возможность не только теоретически изучать поведение сложных экосистем, но и исследовать альтернативные стратегии управления экологической ситуацией. При отсутствии точных формальных правил создаваемая модель не является единственной даже при одинаковых исходных данных.

Как отмечают ведущие специалисты по имитационному моделированию сложных экологических систем, разработка самой модели - только первый шаг. Не менее важным является организация комплекса программ, реализующих модель, структуру и механизм проведения машинных экспериментов. Поэтому правильнее говорить об имитационной системе: человеко-машинной системе, обеспечивающей проведение имитационных экспериментов в режиме диалога.

Назовем основные этапы создания имитационной системы:

1) формулирование задач изучения экологической системы и определение вектора состояния системы;

2) введение системного времени (временного шага), моделирующего ход времени в реальной экосистеме;

3) декомпозиция объекта исследования и построение блочной конструкции имитационной системы;

4) формирование законов и правдоподобных гипотез функционирования экосистемы в целом и по блокам;

5) разработка программ, реализующих блочные составляющие;

6) верификация блоков по фактическим (опытным) данным;

7) объединение блоков на базе стандартного или специально разработанного математического обеспечения;

8) верификация модели в целом и проверка ее адекватности с учетом мнении специалистов-экспертов;

9) планирование математических экспериментов;

10) анализ результатов машинного экспериментирования с пополнением исходного байка данных.