Примеры

На рис. 6.12 показана простейшая сигмоидная кривая, а на рис. 6.13 - J-образные кривые. Рис. 6.13 показывает, что численность трипсов (мелкие насекомые) в благоприятные годы быстро увеличивается, вплоть до конца сезона, после чего их плотность так же быстро снижается. В менее благоприятные годы кривая роста больше похожа на сигмоидную. В общем, J-образную кривую можно рассматривать как неполную сигмоидную кривую, просто лимитирующие факторы среды в этом случае начинают ограничивать рождаемость еще до того, как существенную роль начнут играть внутренние факторы ограничения численности.

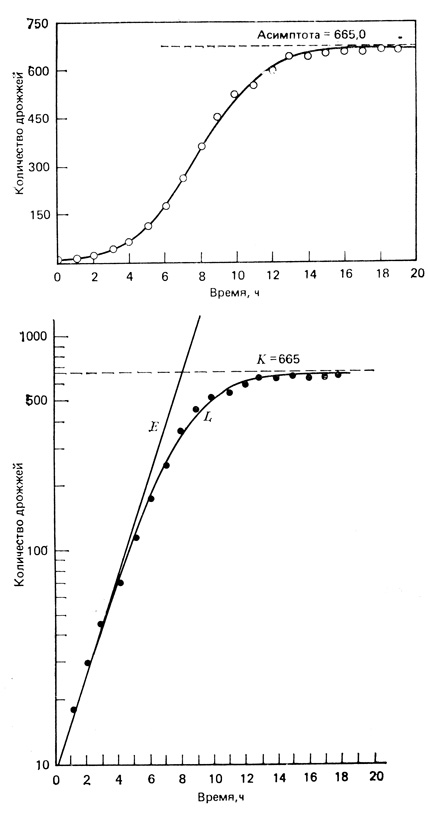
Рис. 6.12. Рост дрожжей в культуре. Простейший случай сигмоидного роста, при котором сопротивление среды (в этом случае вредные факторы обусловлены жизнедеятельностью самих организмов) прямо пропорционально плотности. Светлые кружки - наблюдаемые величины, сплошные линии - кривые, построенные по уравнениям. На верхнем графике рост дрожжей представлен в линейном масштабе и точки ложатся на логистическую кривую. На нижнем графике те же данные представлены в логарифмическом (L) масштабе; приведена также экспоненциальная кривая (Е), показывающая, каким был бы рост при отсутствии самоограничивающих влияний. (Нижний график - по данным Pearl, 1927, верхний - из Allee et al., 1949)

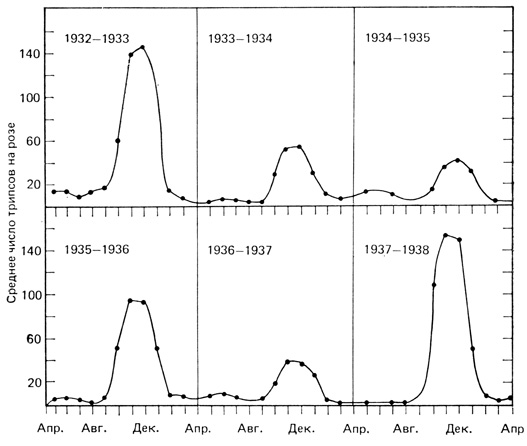
Рис. 6.13. Сезонные изменения численности популяции взрослых трипсов на розах. (График построен по данным из работы Davidson, Andrewartha, 1948)

На рис. 6.12 представлены графики роста дрожжей в арифметическом (вверху) и в полулогарифмическом (внизу) масштабах, соответствующие логистическому уравнению. Обратите внимание на то, что на полулогарифмическом графике кривая больше похожа на перевернутую букву J, чем на букву S. На нижнем графике проведена также экспоненциальная кривая (Е), показывающая, каким мог бы быть рост, не ограниченный размерами культивационного сосуда и плотностью популяции. Эти уравнения представляют собой уже описанные интегральные формы логистического и экспоненциального (с J-образной кривой) уравнений, в которые подставлены реальные значения величин K, a и r. Фактический (наблюдаемый в опыте) рост дрожжей хорошо соответствует логистическому росту, что свидетельствует о раннем проявлении эффекта скученности и его линейной связи с плотностью. Площадь между двумя кривыми на нижнем графике можно принять за количественную меру сопротивления среды. Преимущество полулогарифмического построения заключается в том, что по любому отклонению от прямой линии можно судить об изменении скорости роста популяции (dN/dt). Чем больше изгиб кривой, тем значительнее изменение.

Хотя простой логистический рост, вероятно, характерен лишь для мелких организмов или для организмов с простыми жизненными циклами, S-образные кривые роста наблюдаются и у крупных организмов, когда они интродуцируются на незанятые прежде острова. Пример этому - рост поголовья овец на о. Тасмания (Davidson, 1938) или рост популяции фазанов, интродуцированных на один из островов в Пьюджет-Саунд, шт. Вашингтон (Einarsen, 1945).

Вернемся вновь к не один раз упомянутой в этой книге теме: открытым системам. Расселение - перемещение организмов или их подвижных стадий (семян, спор, личинок и т. п.) на территорию, уже занятую популяцией, или с этой территории - наряду с рождаемостью и смертностью определяет характер роста популяции. Эмиграция - выселение с занимаемой территории - аналогична смертности; иммиграция - аналогична рождаемости. Миграция - периодические уход и возвращение на данную территорию - в разные сезоны влияет на характер кривой роста то как рождаемость, то как смертность. Расселение в большой степени зависит от различных преград и врожденной способности к перемещениям, или подвижности, взрослых особей или стадий их расселения. И, конечно, расселение - это средство колонизации новых или освободившихся пространств. Расселение мелких организмов и пассивных стадий обычно подчиняется экспоненциальной зависимости: в местах, удаленных от места расселения на кратные расстояния, плотность снижается на постоянную величину. Расселение крупных активных животных носит иной характер; оно может закончиться на некотором заданном расстоянии, может иметь форму нормального распределения или принимать другие формы. В исследовании Стюарта (Stewart, 1952), выполненном на окольцованных сипухах, дан хороший пример сочетания случайного расселения с тенденцией миграции к югу. В пределах 100 миль расселение было ненаправленным (т. е. вероятность встретить окольцованную птицу была примерно одинаковой в любой точке и в любом направлении), но за пределами этого расстояния птицы имели явную тенденцию расселяться к югу. Общие обзоры о характере и закономерностях расселения см. в работах Wolfenbarger, 1946, и MacArthur, Wilson, 1967.