Объяснения

Когда тех или иных животных интродуцируют в незанятые области или они сами распространяются туда (как это бывает, например, в начале сезона), часто можно наблюдать характерный тип роста популяции. На графике, построенном в арифметическом масштабе, участок кривой, соответствующей росту популяции, часто имеет S- или J-образную форму (рис. 6.10, А, Б). Интересно отметить, что два основных типа роста, описываемые этими кривыми, сходны с двумя типами метаболизма или роста, которые были описаны для отдельных особей (Bertalanffy, 1957), Однако неясно, существует ли причинная связь между ростом популяций и ростом особей. При нынешнем уровне наших знаний можно только отметить сам факт некоторого сходства в форме кривых. Популяции и сообщества не являются "сверхорганизмами", но могут обладать аналогичными организмам свойствами (гл. 2, разд. 6).

Уравнение, приведенное выше для описания J-образного роста, представляет собой то же самое экспоненциальное уравнение, которое было рассмотрено в разд. 3, с той лишь разницей, что на величину N налагается ограничение. Относительно свободный рост внезапно прекращается, как только популяция исчерпывает какой-либо ресурс (пищу или пространство, когда наступают внезапные заморозки или вмешивается другой сезонный фактор или когда внезапно заканчивается сезон размножения (возможно, например, из-за наступления диапаузы, как описано в гл. 5, стр. 267). По достижении верхнего предела для N плотность может некоторое время оставаться на этом уровне либо сразу же резко падает, что приводит к релаксационно-колебательному характеру изменений плотности, показанному на рис. 6.10, А-1 и А-2. Такое изменение численности, названное Никольсоном (Nicholson, 1954) "триггерным", свойственно, по-видимому, многим природным популяциям, в частности одноклеточным планктонным водорослям во время "цветения", однолетним растениям, некоторым насекомым и, быть может, леммингам в тундре.

Другой, также нередко наблюдаемый тип роста может быть выражен в арифметическом масштабе по отношению к времени S-образной, или сигмоидной, кривой. Характерная форма кривой обусловлена постепенным усилением - по мере нарастания плотности популяции - действия неблагоприятных факторов (сопротивления среды). В этом отношении такой тип роста является прямой противоположностью ранее рассмотренному, при котором популяция начинает испытывать сопротивление среды почти в конце своего роста. По этой причине Никольсон (Nicholson, 1954), говоря о сигмоидном росте, назвал его "обусловленным плотностью". В простейшем случае усиление действия сдерживающих факторов прямо пропорционально плотности. Такой тип роста называют логистическим^*, и он соответствует логистическому уравнению, которое характеризует сигмоидный рост.

^* (Логистическое уравнение было впервые предложено Ферхюльстом (Р. F. Verhulst) в 1838 г.; им широко пользовался Лотка, а затем его "переоткрыли" Пирл и Рид (Pearl, Reed, 1930))

Логистическое уравнение можно записать несколькими способами; три из них вместе с интегральной формой таковы:

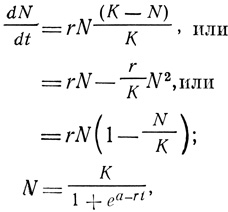
где dN/dt - скорость роста популяции (изменение численности во времени); r - удельная, или внутренняя, скорость роста (обсуждалась в разд. 3); N - величина популяции (численность); К - максимально возможная величина популяции, или верхняя асимптота; е - основание натуральных логарифмов и а - постоянная интегрирования, определяющая положение кривой относительно начала координат. Она численно равна (K - N)/N при t = 0.

Это уравнение отличается от экспоненциального уравнения, приведенного в предыдущем разделе, лишь тем, что оно содержит величину (K - N)/K, (r/K)N² или (1 - N/K). Эти три величины соответствуют трем способам обозначения сопротивления среды, которое порождается вследствие роста самой популяции и по мере того, как величина популяции приближается к емкости среды, вызывает все большее уменьшение потенциальной скорости размножения. В словесной форме эти уравнения означают следующее:

В общем, эта простая модель выводится из трех компонент: константы скорости (r), меры величины популяции (N) и меры того, какая часть доступных лимитирующих факторов не используется популяцией (1 - N/K).

Логистическое уравнение можно записать также в форме, характеризующей скорость прироста на одно поколение, R:

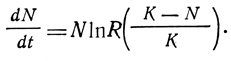
Хотя рост многих популяций микроорганизмов, растений и животных как в лабораторных, так и природных условиях может быть описан сигмоидной кривой, это вовсе не означает, что такие популяции растут согласно логистическому уравнению. Существует много математических уравнений, решение которых можно представить графически в форме сигмоидных кривых. Почти любое уравнение, в котором увеличение отрицательного воздействия находится в какой-то зависимости от плотности, дает сигмоидную кривую. Как отметил Вигерт (Wiegert, 1974), логистическая кривая представляет собой своего рода минимальный сигмоидный рост, поскольку лимитирующие эффекты и пространства, и ресурсов сказываются с самого начала роста (т. е. максимальная удельная скорость роста достигается только при нулевой плотности). В большинстве случаев менее ограниченный рост ожидается в начальной фазе, а затем по мере увеличения плотности скорость роста медленно понижается. Рис. 6.11 иллюстрирует представление о том, что логистическая кривая отражает наиболее медленный, а экспоненциальная кривая - наиболее быстрый тип роста. Следует ожидать, что рост большинства популяций занимает промежуточное положение.

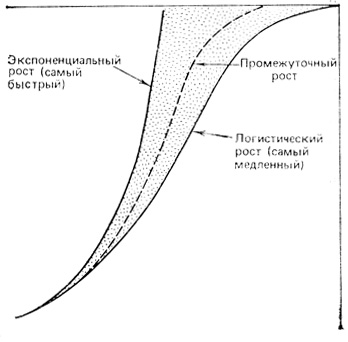
Рис. 6.11. Кривые, показывающие теоретически самое быстрое (экспоненциальное) и самое медленное (логистическое) увеличение численности популяции. Максимальные скорости роста и минимальные плотности одинаковы. Между кривыми находится область (заштрихована), соответствующая росту большинства популяций. (По Wiegert, 1974)

В популяциях высших растений и животных, имеющих сложные жизненные циклы и длительный период индивидуального развития, наблюдается несовпадение во времени увеличения плотности и воздействия лимитирующих факторов. Говоря словами Никольсона (Nicholson, 1954), этот тип роста можно назвать "обусловленным плотностью с запаздыванием". В таких случаях получается более вогнутая кривая роста (необходимо больше времени, чтобы проявился эффект рождаемости), популяция почти всегда "перепрыгивает" верхнюю асимптоту и испытывает колебания численности, прежде чем стабилизироваться на уровне емкости среды (см. рис. 6.10, кривая Б-2). Для того чтобы учесть два типа временных задержек: 1) время до начала прироста при благоприятных условиях и 2) время, нужное для того, чтобы в неблагоприятных условиях перенаселения начали изменяться рождаемость и смертность, было предложено большое число модифицированных логистических уравнений. Обозначив эти задержки соответственно как t - t₁ и t - t₂, получаем

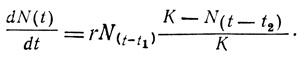
При исследовании этого варианта уравнения на аналоговом устройстве или мини-ЭВМ получается, что плотность возрастает с овершутом ("перепрыгивает" асимптоту) и колеблется с уменьшающейся во времени амплитудой, как показано на рис. 6.10 кривая Б-2.

Обозначения dt (мгновенное время) и Δt (дискретный интервал времени), использовавшиеся в разделах 2, 3 и 4, отражают два распространенных математических подхода при моделировании популяций и экосистем: один из них основан на применении систем дифференциальных уравнений, а другой - систем разностных уравнений. Дифференциальные уравнения более удобны в чисто математическом плане, вероятно, поэтому им уделяется столько внимания в учебных курсах вычислительной математики. В то же время разностные уравнения лучше соответствуют способу получения исходных данных (в дискретные интервалы времени) и структурам кривых роста популяций у видов с дискретными поколениями. Для сравнения повторим дифференциальные уравнения J- и S-образных кривых роста популяций и запишем для каждого случая соответствующее разностное уравнение. Дифференциальное уравнение непрерывного экспоненциального роста имеет вид

а разностное уравнение дискретного экспоненциального роста

где N_t+1 - изменение за данный временной интервал; λ - мультипликативный коэффициент роста на поколение или на какой-то другой выделенный период (это есть конечная скорость роста, введенная в разделе 3, с. 29, она аналогична r, внутренней скорости роста). r = lnλ, так что λ = e^r, что и отражает замена λ в уравнении (3). При росте численности популяции λ должна быть больше 1, а r больше 0, в противном случае численность популяции экспоненциально уменьшается и в конце концов она вымирает.

Дифференциальное уравнение для логистического (зависимого от плотности или сигмоидного роста) имеет вид

а разностное уравнение для зависимого от плотности роста -

В качестве аналогов уравнений логистического и других типов зависимого от плотности роста было предложено несколько типов разностных уравнений (см. May, 1976; May и Oster, 1976). Примечательно, что разностные уравнения можно использовать в том виде, в каком они есть, не интегрируя их как дифференциальные уравнения. Сравните уравнение (5) с интегральной формой логистического уравнения, указанного выше.

Выбор подхода зависит от того, что интересует в данной задаче: характер изменения некоторой величины или скорость ее изменения. В последнем случае лучше использовать дифференциальные уравнения.

Почти все математические модели роста популяций сильно уязвимы вследствие того, что они оперируют в закрытых системах, не имеющих входа и выхода. Моделируется только само перенаселение и другие внутренние факторы. Как не раз обсуждалось в гл. 2 и 3, реальный мир состоит из открытых систем, в которых большую роль играют среда на входе и среда на выходе (см. рис. 2.1). Эта ошибка особенно заметна при моделировании или предсказаниях характера роста популяций человека. Эдвард Диви (Deevey, 1958) много лет назад отметил, что при отсутствии "внешнего" управления, такого, как систематическое планирование семьи, рост народонаселения должен был бы, скорее всего, следовать некоей кривой с овершутом и колебаниями, поскольку механизмы ограничения перенаселения срабатывают с временными задержками. По-видимому, быстро растущие города, зависящие от мощных внешних источников энергии, поступления пищи, воды и общих ресурсов жизнеобеспечения, особенно подвержены в разной степени чередованию взлетов и кризисов; это определяется факторами на входе и тем, насколько отдельные граждане и правительственные органы могут предвидеть грядущие условия и осуществлять соответствующее планирование. Так, на ранних стадиях роста города, когда экологические условия благоприятны (пространство и ресурсы доступны и недороги) и когда потребность в обслуживании (вода, переработка отходов, улицы, школы и т. д.) мала, численность населения растет быстро (при этом часто главным образом за счет иммиграции), что отвечает J-образной кривой роста. Но спустя некоторое время (до срабатывания временной задержки) школы и жилой фонд оказываются перегруженными, увеличиваются потребности в обслуживании, наблюдается рост цен и становятся ощутимыми общие нарушения в масштабах всего хозяйства. В отсутствие отрицательной обратной связи, такой, какая встроена в простую логистическую зависимость или какую можно включить в рациональное планирование, города будут расти слишком быстро, что неблагоприятно скажется на их состоянии и приведет к упадку.