Объяснения и примеры

Три типа распределения особей внутри популяции упрощенно показаны на рис. 6.19. В каждом прямоугольнике находится примерно одинаковое число особей. При групповом распределении (В) группы могут быть одинакового или разного размера (как на рисунке) и распределяться случайно (как показано) или в свою очередь объединяться в скопления, между которыми остаются обширные незанятые пространства. Иными словами, существует пять типов распределения: 1) равномерное; 2) случайное; 3) случайное групповое; 4) равномерное групповое и 5) групповое, с образованием скоплений групп. Все эти типы, несомненно, встречаются в природе. Как явствует из рис. 6.19, малые выборки, взятые из трех представленных популяций, дадут совершенно различные результаты. При малой выборке из популяции с групповым распределением будут получены либо слишком низкие, либо слишком высокие величины плотности в пересчете на всю популяцию. Таким образом, при изучении популяций с групповым распределением необходимо более тщательное планирование эксперимента, а число выборок должно быть большим, чем в случае, если распределение не групповое.

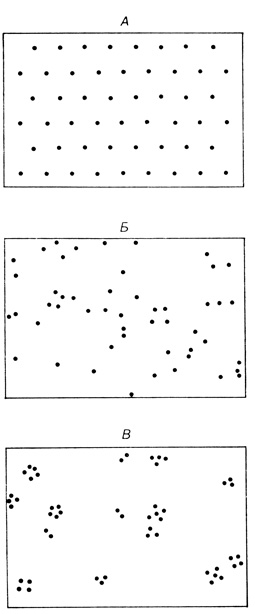
Рис. 6.19. Три основных типа распределения особей, пар или групп особей в популяции. А. Равномерное распределение. Б. Случайное распределение. В. Групповое распределение (распределение групп нерегулярно)

Случайному распределению соответствует нормальная, или колоколообразная, кривая, на которой основаны стандартные статистические методы. Распределение такого типа можно ожидать в природе в тех случаях, когда на популяцию одновременно воздействуют многочисленные, но слабые факторы. (Вспомните разд. 5, в котором обсуждалась возможная случайная основа циклических колебаний.) Если же, как это обычно бывает, преобладает лишь несколько основных факторов (вспомните принцип лимитирующих факторов) или если у растений и животных наблюдается сильная тенденция к образованию скоплений для (или вследствие) размножения и других целей, то вряд ли следует ожидать полностью случайного распределения. Однако встречаемые иногда в природе неслучайные или "контактные" распределения можно рассматривать как результат случайного распределения групп, содержащих разное число особей (как на рис. 6.19, В), или же группы могут быть распределены равномерно (или по крайней мере не совсем случайно). Иными словами (мы берем крайний случай), лучше определить каким-либо выборочным методом число муравейников (используя муравейник как популяционную единицу), а затем определить число муравьев на 1 муравейник, нежели пытаться определить количество муравьев непосредственно, используя метод случайных выборок.

Предложено несколько методов, позволяющих определить тип распределения особей в пространстве и степень скученности особей в популяции (когда это не самоочевидно), однако здесь предстоит решить еще много задач. В качестве примеров можно упомянуть два метода. Один из них состоит в сравнении фактических частот встречаемости групп животных с разной численностью, выявленной в серии выборок, с членами ряда Пуассона, задающего частоты, с которыми должны встречаться группы из 0, 1, 2, 3, 4, ... n особей, при случайном распределении. Так, если частота малых групп (включая пустые выборки) и обильных групп выше, а частота средних по величине групп ниже, чем ожидаемая, то мы имеем дело с групповым распределением. Противоположная ситуация характеризует равномерное распределение. При определении значимости наблюдаемого отклонения от кривой Пуассона проводят статистический анализ, однако этот общий метод неудобен тем, что на результат может влиять величина выборки. Один из примеров использования метода Пуассона для проверки случайного распределения пауков показан в табл. 6.5. На восьми из одиннадцати площадок пауки распределялись случайно. Неслучайное распределение имело место на площадках с наименее однородной растительностью.

Для случайных распределений характерно одно общее свойство, состоящее в том, что дисперсия (V) равняется среднему (m). Если дисперсия больше среднего, то распределение групповое, если же дисперсия меньше среднего, то распределение равномерное (регулярное). Таким образом, при случайном распределении

Если при использовании стандартных критериев значимости оказывается, что отношение дисперсия/среднее больше единицы, то распределение групповое, если это отношение значимо меньше единицы, то мы имеем дело с равномерным распределением, и если отношение равно единице - со случайным распределением. Такой подход иллюстрируется также в табл. 6.5.

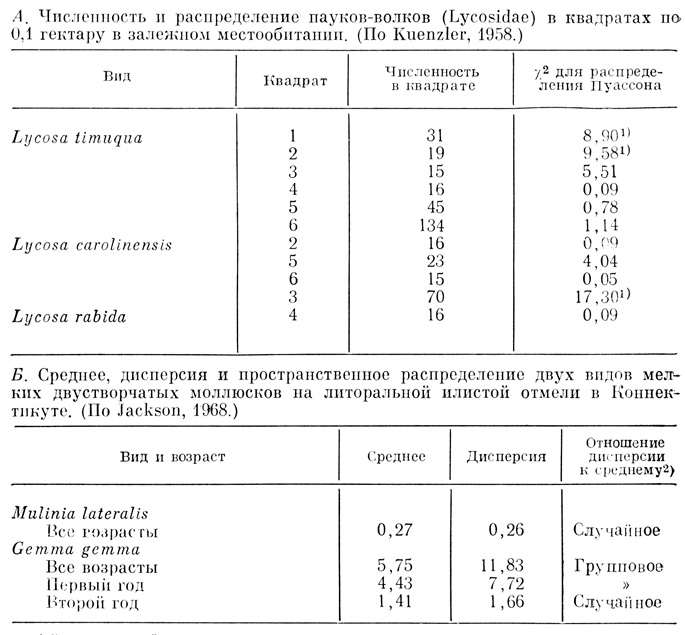
Таблица 6.5. Случайное и неслучайное пространственное распределение пауков и двустворчатых моллюсков

¹ (Значимо на 5-процентном уровне, т. е. не случайно. Во всех остальных квадратах распределение случайно.)

² (Если отличие от единицы не значимо (на 5-процентном уровне), то распределение случайно; если значимость отличия от единицы меньше 1%, то это свидетельствует о групповом (агрегированном) распределении.)

Другой метод, предложенный Дайсом (Dice, 1952), заключается в измерении каким-либо стандартным способом расстояния между особями. Если построить далее график, на котором квадратные корни из этих расстояний представлены как функция частот, то форма полученного многоугольника будет свидетельствовать о характере распределения. Симметричный многоугольник частот (иными словами, нормальная колоколообразная кривая) свидетельствует о случайном, скошенный вправо - о равномерном, скошенный влево - о групповом распределении (особи находятся ближе друг к другу, чем ожидалось). Численную меру степени "скошенности" можно оценить количественно. Этот метод, разумеется, лучше применять для растений или неподвижных животных, но его можно использовать и для оценки распределения в пространстве колоний или жилищ животных (нор лис и грызунов, гнезд птиц и т. д.).

Личинки мучных хрущаков обычно случайно распределены в своей очень однородной среде: их наблюдаемое распределение соответствует распределению Пуассона (Park, 1934). Одиночные паразиты или хищники, такие, как пауки, рассматриваемые в табл. 6.5, характеризуются иногда случайным распределением (и они часто проводят время, занимаясь случайным поиском хозяина или жертвы). Джексон (Jackson, 1968) сообщил о случайном характере распределения особей двустворчатого моллюска Mulinia lateralis на илистой литорали. Так же были распределены двухлетние особи Gemma gemma, однако для однолетних особей и всей популяции Gemma закономерность оказалась иной: в связи с яйцеживорождением (т. е. личинки развиваются в теле самки) распределение этих животных было групповым. Результаты этого исследования приведены в табл. 6.5, Б. Обратите внимание на то, что в популяции со случайным распределением дисперсия близка к среднему, а в популяции с групповым распределением - значимо больше среднего. Илистое дно - очень гомогенная среда обитания, и межвидовая конкуренция здесь выражена слабо. Оба этих обстоятельства благоприятствуют случайному распределению.

У деревьев в лесу, достаточно высоких, чтобы их кроны образовали часть общего полога, распределение может быть равномерным, поскольку конкуренция за свет у деревьев столь велика, что у них наблюдается тенденция отстоять друг от друга на расстояния, которые "скорее регулярны, нежели случайны". Поля зерновых культур, фруктовые сады и посадки сосны могли бы служить еще лучшими примерами. Кустарники в пустыне часто распределяются очень равномерно, почти так, словно их специально сажали рядами. По-видимому, дело здесь в интенсивной конкуренции (быть может, связанной, в частности, с выделением антибиотиков) в среде с недостаточной влажностью. Тенденция к более равномерному распределению у некоторых животных может быть обусловлена территориальностью (разд. 9).

За примерами группового распределения и пятнистой среды обитания читателю далеко ходить не придется. Из многих изученных Коулом (Cole, 1946, 1946а) беспозвоночных, обитающих в лесной подстилке, только для пауков было характерно случайное распределение. В другой работе Коул отметил, что случайное распределение удалось установить только для 4 из 44 видов растений. Все остальные виды были в той или иной степени объединены в группы.

Более подробно статистика пространственного распределения элементов популяций рассмотрена в работах Скеллама (Skellam, 1952), Гудолла (Goodall, 1970) и Пиелу (Pielou, 1975).