Объяснения

Такие показатели, как рождаемость, смертность и возрастное распределение, весьма важны, но каждый из них сам по себе мало что дает; в частности, по каждому из них нельзя судить о росте популяции как целого, о характере изменений, которые произойдут при изменении условий среды, о максимальных возможностях популяции и отличии их от ее реальных возможностей. Для обозначения максимального репродуктивного усилия Чепмен (Chapman, 1928) предложил термин биотический потенциал. Он определил его как "врожденное свойство организма к размножению и выживанию, т. е. к увеличению численности. Это своего рода алгебраическая сумма числа молодых особей, производимых за каждый цикл размножения, числа циклов размножения за данный период времени, соотношения полов и общей способности организма выживать при данных физических условиях". Однако весьма общий характер определения биотического, или репродуктивного, потенциала, данного выше, привел к тому, что разные исследователи вкладывают в него разный смысл. Для одних он означает некую туманную способность к размножению, скрытую в популяциях и, к счастью, никогда не проявляющуюся в полной мере благодаря воздействию окружающей среды ("в неконтролируемых условиях потомство одной пары мух через несколько лет весило бы больше, чем земной шар"). Другие представляют его просто и более конкретно, как то максимальное число яиц, семян, спор и т. д., которое может продуцировать наиболее плодовитая особь, хотя обычно такое представление имеет мало значения применительно к популяции, поскольку в большинстве популяций все особи не способны постоянно поддерживать максимальную продуктивность.

Лотка (Lotka, 1925), Даблин и Лотка (Dublin, Lotka, 1925), Лесли и Рэнсон (Leslie, Ranson, 1940), Бирч (Birch, 1940) и другие исследователи выразили это довольно широкое представление о биотическом потенциале в математических терминах, понятных на любом языке (однако подчас лишь с помощью хороших математиков). Хорошо сказал по этому поводу Бирч: "Если попытаться количественно выразить "биотический потенциал" Чепмена с помощью всего лишь одного показателя, то, по-видимому, лучше всего для этого использовать параметр r, поскольку он характеризует внутренне присущую животным способность к увеличению численности в отсутствие лимитирующих факторов среды". Как будет отмечено далее, показатель r часто используется также для количественного выражения "репродуктивной приспособленности" в генетическом смысле.

Если вспомнить о кривых роста, обсуждавшихся в разд. 2, то r представляет собой удельную скорость роста (ΔN/NΔt) только для случая экспоненциального роста популяции. Уравнение (3), приведенное в разд. "Определения", есть уравнение прямой. Следовательно, величину r можно определить графически. Если кривую роста вычерчивать в логарифмическом или полулогарифмическом масштабе, то при экспоненциальном росте график зависимости логарифма численности популяции от времени будет иметь вид прямой линии, а r будет наклоном этой прямой. Чем круче наклон, тем выше внутренняя скорость роста. На рис. 6.9 одна и та же кривая роста построена двумя способами: слева численности (N) отложены на арифметической, а справа - на логарифмической шкале (правый график на полулогарифмической шкале). В этом примере гипотетическая популяция микроорганизмов шесть дней находилась в состоянии экспоненциального роста, причем каждые двое суток происходило десятикратное увеличение численности. Наклон прямой на полулогарифмическом графике равен 1,15; это и есть величина r. В этом нетрудно убедиться, подставляя в уравнение (3) две любые величины численности популяции, например, на 2- и 4-е сутки:

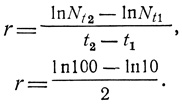
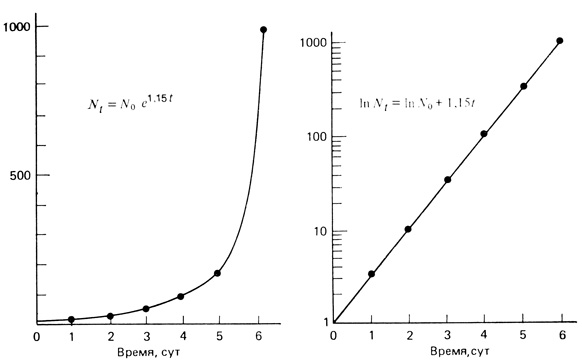
Рис. 6.9. Кривая роста одной и той же популяции, построенная двумя разными способами. Число особей (N) отложено в арифметическом (слева) и логарифмическом масштабе (справа). Рассматривается гипотетическая популяция микроорганизмов, растущая экспоненциально в течение 6 суток; в этот период каждые два дня численность возрастала в 10 раз. Объяснения уравнений см. в тексте

Воспользовавшись таблицей натуральных логарифмов, получаем

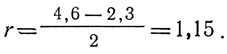
Чрезвычайно широкий диапазон значений биотического потенциала выявляется особенно отчетливо, если выражать его с помощью величины, показывающей, во сколько раз увеличится численность при экспоненциальном росте или какое время требуется для удвоения популяции. Эти два параметра математически выводятся из внутренней скорости роста:

Конечная скорость прироста: λ = e^r; log_e λ = r; λ = antilog_er.

Время удвоения: t = log_e2/r = 0,6931/r

(эту величину мы получаем из уравнения (2), принимая N_t/N₀ = 2).

При максимальной внутренней скорости роста время удвоения для популяции мучного хрущака в оптимальных лабораторных условиях составляет меньше недели (см. Leslie, Park, 1949). Для человека время удвоения в 1968 г. составляло 35 лет (Ehrlich, Ehrlich, 1970), однако в некоторых странах население удваивается быстрее. Смит (Smith, 1954) полагает, что r и соответственно периоды удвоения в живой природе различаются более чем на шесть порядков.

Коэффициент роста популяции r не следует путать с чистой скоростью размножения R₀, рассмотренной в разд. 1 (см. табл. 6.3). R₀ связано со временем генерации и не подходит для сравнения разных популяций, характеризующихся различным временем генерации. Однако среднее время генерации (Т) связано с R₀ и r следующим образом:

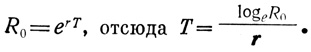
Зависимость между Т, R₀ и r для популяций различных животных графически представлена на стр. 52 книги Слободкина (Slobodkin, 1962). В природных популяциях в непродолжительные периоды времени, когда пища имеется в изобилии, отсутствуют скученность, враги и т. д., нередко проявляется экспоненциальный характер роста. В таких условиях популяция в целом растет с огромной скоростью, хотя при этом каждый организм размножается с той же скоростью, что и раньше, а удельная скорость роста постоянна. "Цветение" планктона, упомянутое в предыдущих главах, вспышки численности вредителей, рост бактерий на свежей культуральной среде - служат примерами ситуаций, в которых рост может быть логарифмическим. Подобный характер изменений отмечается и для многих других явлений, например поглощения света, мономолекулярных химических реакций, роста сложных процентов. Очевидно, что экспоненциальный рост не может продолжаться очень долго, а часто и вовсе не реализуется. Взаимодействия с другими популяциями, а также сопротивление внешней среды быстро снижают скорость роста и различным образом влияют на характер роста популяции.